近日，betvlctor网页版登录量子材料科学中心宋志达课题组与合作者对魔角石墨烯的超导机制提出了一种理论，该理论解释了超导何以发生在掺杂的关联（莫特）绝缘体中，并解释了多个实验上观测到的非常规超导特征，包括向列相、V型能隙、短相干长度、超导转变温度T_c显著低于配对能隙等。该理论认为，尽管配对通道不同，魔角石墨烯中的配对机制十分类似于三价富勒烯化合物（A₃C₆₀）中的配对机制，而后者被认为是一种电声子耦合引起的、库伦排斥协同的非常规超导。在技术上，该理论利用场论中的Ward恒等式证明：尽管魔角石墨烯中的库伦排斥远强于光学声子引起的微弱吸引相互作用，但重整化后的准粒子相互作用必然存在配对项。相关成果于2024年9月30日以“魔角石墨烯超导中的分子配对”（Molecular pairing in twisted bilayer graphene superconductivity）为题发表于《物理评论快报》（Physical Review Letters）。

自2018年魔角石墨烯中的超导被发现以来，其非常规特性受到了凝聚态研究者的广泛关注。此类特性不能由传统的Bardeen-Cooper-Schrieffer（BCS）机制所解释，且部分性质与铜氧化物高温超导体类似。

魔角石墨烯的低能电子态形成拓扑平带，许多理论研究（包括宋志达之前的工作）都曾指出此平带不存在对称的局域瓦尼尔表象。然而，宋志达课题组对该体系的持续研究发现，此拓扑平带可由一组局域轨道（f-电子）外加巡游狄拉克电子（c-电子）所描述，并由此于2022年提出了魔角石墨烯的拓扑重费米子模型【1】。有效f-电子轨道相对于摩尔超晶格很局域，但相对于微观碳晶格却很扩展，可以视为包络了成百上千个原子的“分子轨道”。电子间的库伦排斥在f-电子轨道上占主导地位，使得在位电荷涨落被有效压制。因此，f-电子轨道扮演了凝聚态重费米子问题中局域磁矩的角色。在整数填充时，这些局域磁矩通过Ruderman–Kittel–Kasuya–Yosida（RKKY）相互作用形成长程序，这一视角很好地解释了之前的许多理论计算，并与实验上看到的关联绝缘体一致。在非整数填充时，近藤屏蔽发生，系统进入重费米液体相，这一视角可以解释STM实验上看到的零能峰、压缩率实验上测到的熵、以及随升温而出现局域磁矩的所谓Pomeranchuck效应【2】。

该工作研究了重费米液体相在电声子耦合作用下的稳定性。其中，最重要的耦合来自引起石墨烯谷间电子散射的声子模式【3】，它导致了f-电子轨道上的“反洪特”劈裂，可降低谷间配对的能量。综合考虑反洪特劈裂与其它库伦相互作用后，研究者发现f-电子轨道上的两电子基态为d波自旋单态。然而，由于库伦排斥的主导作用，两电子能总是正定的，因此裸粒子无法形成超导配对。

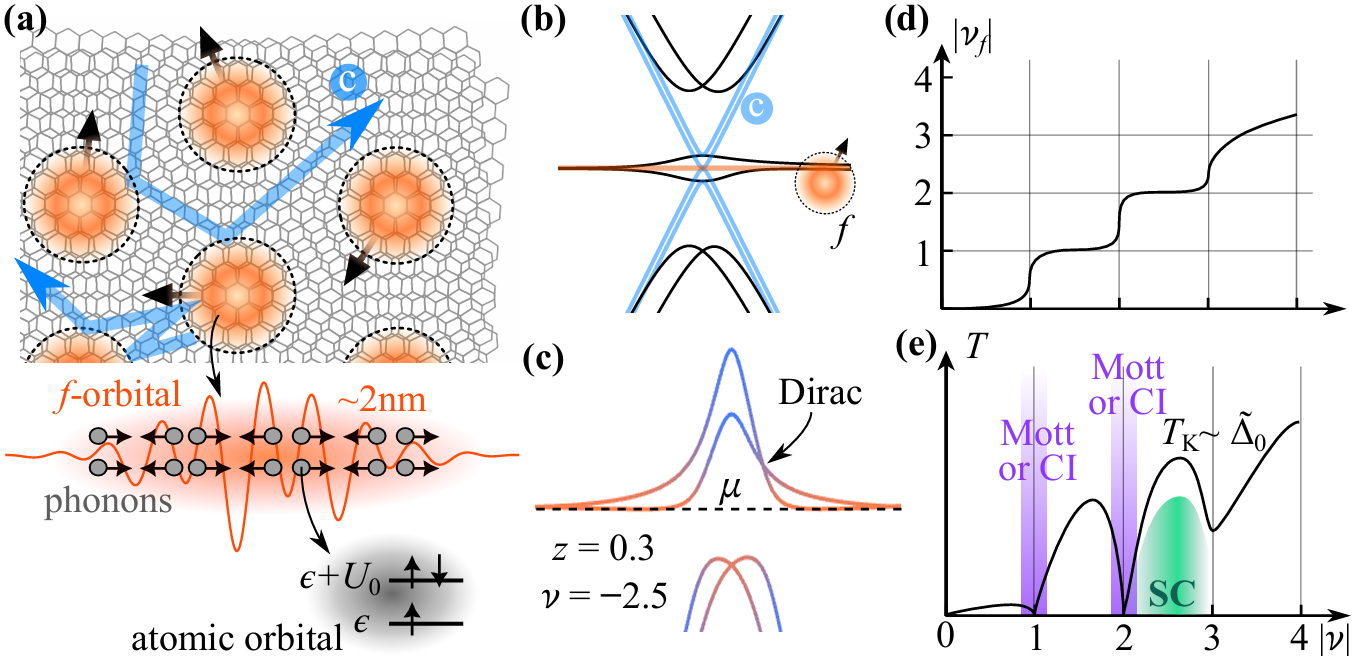
图1.魔角石墨烯作为重费米子问题。（a）中橙色包络示意f-电子轨道。声子振动导致反洪特耦合。（b，c）无关联和强关联的重费米子能带。（d，e）f电子占据数与近藤温度随掺杂的变化示意。超导序一般出现在|v|=2.5附近的穹顶状区域中。

上述特征高度相似于C₆₀中的低能分子轨道：一种被称为动力学Jahn-Teller效应的电声子耦合对C₆₀的分子轨道贡献了类似的反洪特劈裂。虽然其强度远弱于库伦排斥能，在A₃C₆₀晶体中+3价的C₆₀分子却可以在40K左右的温度形成配对并超导。被学界广泛接受的理论是：由于在位电荷涨落被压制，高度关联的准粒子感受到的有效库伦排斥也被大幅削弱。相比之下，反洪特劈裂对电荷涨落较不敏感，可以胜过库伦排斥，诱发超导。A₃C₆₀启发了作者们在魔角石墨烯中寻找类似的配对机制。

魔角石墨烯具有更多的内禀自由度，直接进行多体数值计算十分具有挑战性。然而，作者们借助场论中的Ward恒等式巧妙地避开了这一困难【4】。物理图像上，该方法基于局域费米液体的两个性质。第一个性质是准粒子与裸粒子携带完全一样的守恒荷，守恒荷由对称性给出，包括电荷、自旋、角动量等。第一个性质使得裸粒子的守恒荷的极化率可以用准粒子的相互作用（即全顶角函数）来表达。第二个性质是守恒荷极化率的一些渐进行为仅由两粒子基态决定，而这是已知的。因此，可用极化率的渐进行为反推准粒子的有效相互作用。借助Ward恒等式，这种推导是严格的。通过上面给出的相互作用，作者证明，局域相互作用在近藤温度T_K较低时必然存在配对通道，且配对势与T_K相当。计算表明能量最低的配对为时间反演对称、旋转破缺的向列d波单态。由此，该理论解释了电声子诱发的超导何以与强库伦排斥引起的关联（莫特）绝缘体共存。

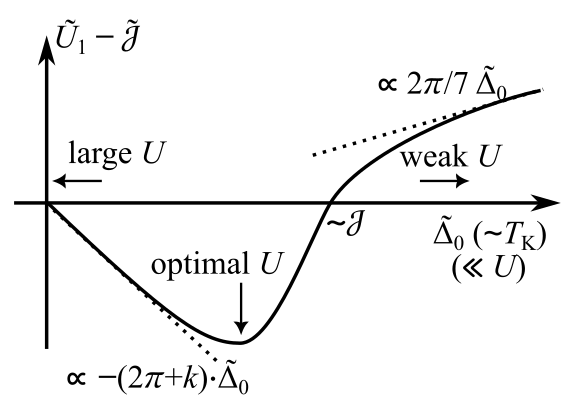
图2.有效配对势作为近藤温度T_K的函数，其中J是反洪特耦合。当T_K远大于J时，有效相互作用是排斥的。当T_K大约降低至J时，有效相互作用变为吸引。当T_K趋于零时，配对势也趋于零。

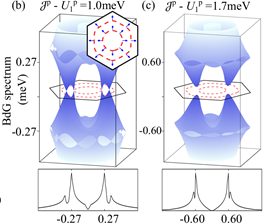
图3.超导相的BdG准粒子能谱，态密度为V型。

由于重费米液体的费米面含有Dirac巡游电子的分量，两层费米面各自带有𝜋贝利相位。这使得尽管微观的配对通道为向列d波单态，其投影在费米面上却表现出向列p波的形状：每个费米面上具有一对相差180度的配对节点。这将表现为向列相的对称性、V字型的隧穿谱等行为。

最后，由于配对在空间上是局域的、且配对势与重费米子动能相当，该超导相更接近强耦合的玻色爱因斯坦-凝聚（BEC）图象，而非BCS图像。在此理论中，配对的相干长度由近藤云的尺寸来决定，其大约为几个摩尔晶格的量级，与实验上看到的短相干长度（与载流子平均距离相当）一致。同时，由于配对的局域性，超导的相位刚度很低，自然会导致超导转变温度T_c显著低于配对能隙。实验上T_c仅为配对能隙的二十五分之一。

审稿人认为该研究“是解决魔角石墨烯超导问题的绝妙想法和新颖方法，意外地将其与最著名和最可靠的“非常规”配对例子之一（A₃C₆₀）联系了起来。”

betvlctor网页版登录量子材料科学中心2021级博士生王一杰、2022级博士生周耿栋为本文共同第一作者，宋志达为通讯作者，合作者还包括普林斯顿大学物理系助理教授廉骉、加州理工学院应用物理与材料科学系博士后彭士宇。该工作得到了国家自然科学基金委面上项目、国家重点研发计划、科技创新2030——“量子通信与量子计算机”重大项目的支持。

原文链接：https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.133.146001

参考文献：

【1】Z.-D. Song and B. A. Bernevig, Magic-Angle Twisted Bilayer Graphene as a Topological Heavy Fermion Problem, Phys. Rev. Lett. 129, 047601 (2022).

【2】G.-D. Zhou, Y.-J. Wang, N. Tong, and Z.-D. Song, Kondo phase in twisted bilayer graphene, Phys. Rev. B 109, 045419 (2024).

【3】Y.-J. Wang, G.-D. Zhou, B. Lian, and Z.-D. Song, Electron Phonon Coupling in the Topological Heavy Fermion Model of Twisted Bilayer Graphene, arXiv:2407.11116 (2024).

【4】Y.-J. Wang, G.-D. Zhou, S.-Y. Peng, B. Lian, and Z.-D. Song, Molecular Pairing in Twisted Bilayer Graphene Superconductivity, Phys. Rev. Lett. 133, 146001 (2024).