betvlctor网页版登录量子材料科学中心刘雄军教授和该组访问学者潘建松博士(上海交通大学维尔切克量子中心博士后）、美国匹兹堡大学刘文胜教授合作，理论预言具有拓扑内蕴机制的非常规第二类Nambu-Goldstone玻色子的存在，并提出基于光晶格实现和观测的方案。该工作将凝聚态物理中朗道对称破缺理论和拓扑理论两大框架内蕴结合，预言新的量子相的存在，并对Nambu-Goldstone的有关机理产生新的理解。该工作发表在最近一期的《物理评论快报上》：J.-S. Pan, V. W. Liu, and X.-J. Liu, Phys. Rev. Lett. 125, 260402 (2020)。

如何刻画量子物质基本相是过去半个多世纪凝聚态物理最基本的主题，并形成朗道-金茨堡对称破缺理论和拓扑理论两大基本理论框架。在对称破缺理论中，物质发生相变对应系统的对称性发生改变，同时伴随局域序参量的产生。熟悉的例子比如铁磁体，其高温下体系内的自旋磁矩由于热涨落而混乱分布，所有磁矩整体具有旋转对称性（各向同性），没有自发磁化。当温度调到临界温度以下，磁矩间相互作用会克服热涨落，使得自旋倾向于平均指向共同的方向，即自发磁化方向，因而系统不再各向同性，失去旋转不变性。这导致了旋转对称的自发破缺，而自发磁化即为描述铁磁相的序参量。和对称破缺相不同，拓扑相变不对应对称性的破缺，相应拓扑物相也不由局域序参量刻画，而是由表征体系整体性质的拓扑不变量表征。著名的例子包括量子霍尔效应，以及近些年发现的时间反演对称拓扑绝缘体等。由于存在基本概念的巨大差别，对称破缺相和拓扑相可对应完全不同的重要基本物理。对于破坏连续对称性的物相（如铁磁相），体系出现无能隙的低能激发，被称作Nambu-Goldstone玻色子。在拓扑物相中，系统可存在体能隙，而边界会出现无能隙的边界态。这种边界态和体拓扑对应，称为体-边对应关系，并受系统的体拓扑保护。

通常认为，对称破缺和拓扑理论作为两个不同的基本理论框架，所刻画的基本物相从根本上相互区别。是否存在将对称破缺和拓扑理论内蕴结合才能刻画的基本物相？这显然是十分有意义的基本问题。需要注意，凝聚态物理中熟知的拓扑超导并不属于这类基本物相。因为在拓扑超导中，虽然超导属于对称破缺相，同时又具有非平凡拓扑，但超导和拓扑在其中是各自独立的概念，二者只是“平凡地”加在一起，而非内蕴的结合。在本工作中，刘雄军和合作者偶然发现，在由一种特殊的s-p轨道形成的超流态中出现非常规的第二型Nambu-Goldstone玻色子【见图示】。具体而言，根据能谱特征，Nambu-Goldstone玻色子存在两种不同基本类型，即第一型（具有奇数能量-动量色散关系）和第二型（具有偶数能量-动量色散关系）。基于由Nielsen, Chadha, Watanabe, Brauner, Murayama等建立的传统理论，第二型Nambu-Goldstone玻色子的出现需要体系同时发生两种互不对易的对称的自发破缺。然而，在这项工作所研究的s-p轨道超流态中，自发破缺的对称全部相互对易，因此所发现的非常规的Nambu-Goldstone玻色子无法仅仅基于传统的对称破缺理论解释。作者们发现，这种非常规第二型Nambu-Goldstone玻色子可以由超流态中基于自发破缺的对称所生成的基态简并空间经过投影后出现的拓扑相变来刻画。为此，他们引入“破缺对称投影空间中的拓扑相变”的概念。作者们证明，在离开拓扑相变点时，Nambu-Goldstone玻色子呈现线性色散，属于第一型。在拓扑相变发生时，超流态部分轨道分量在简并基态的参数空间出现零点，类比为拓扑相变的能隙关闭点。该特征导致Nambu-Goldstone玻色子的能谱从线性类型转变为平方类型，即转变为第二类。作者们据此建立了由自发对称破缺和拓扑理论共同刻画的导致非常规Nambu-Goldstone玻色子的一般化理论。和过去不同，这里的拓扑态必须内蕴地定义在自发对称破缺之上，与以往的概念具有本质区别。

该工作首次将凝聚态物理中朗道对称破缺理论和拓扑理论两大框架内蕴结合，预言新的量子相的存在，对Nambu-Goldstone的有关机理产生新的理解，并具有潜在深刻的意义。潘建松博士是文章第一作者。刘雄军教授和刘文胜教授是文章的通讯作者。该工作得到国家自然科学基金委，科技部和中国科学院等支持。

(a) s-p轨道超流的相图；（b-e）Nambu-Goldstone玻色子能谱，其中的第二类非常规Nambu-Goldstone玻色子在（a）图中M和T的相边界得到。

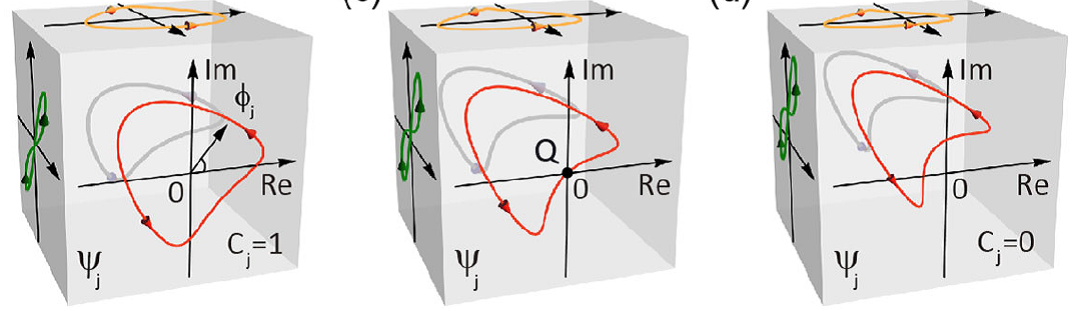
从M到T相之间对称破缺的性质没有发生改变，但在简并基态对应的参数空间之间发生拓扑转变。