输运是物理学的最基本的现象之一，新兴的各向异性输运长期以来在凝聚态物理的发展中发挥着重要作用。近期，betvlctor网页版登录量子材料科学中心进藤龙一（Ryuichi Shindou）课题组的博士研究生肖振宇等人首次提出了能带拓扑和无序的共存会引发了一种新的热力学准局域相。该相表现为波函数在一个空间方向上是非局域的，而在其他两个空间方向上则呈指数衰减。这与传统的金属相和安德森局域相有所不同。这一发现打破了物理学中关于波函数指数局域化在所有空间方向上同时发生的普遍共识。在准局域相中，电导沿着关联长度分散的方向随着系统尺寸按非欧姆定律增长，而沿着其他方向，在热力学极限下电导则消失。在论文中，肖振宇等人通过精确的数值计算关联长度的临界指数、临界无序强度和电导，并比较了有无拓扑模型中这些量的差异，确立了这些发现。为了进一步推广这一新颖相，他们引入了低维逆参与率（lower-dimensional inverse participation ratio），并利用它来推导准局域相在任意空间维度和对称类下的存在标准。

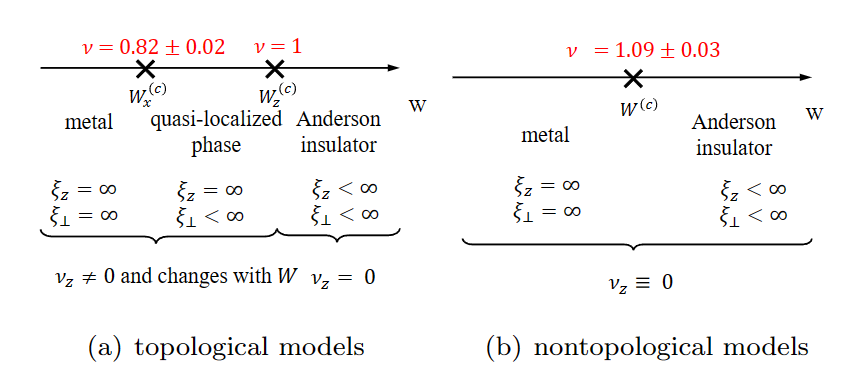
图1存在能带拓扑（a）和不存在能带拓扑（b）的模型在无序下的相图以及相变临界指数的对比。

除了准局域相的发现外，论文还首次发现了由拓扑引起的安德森转变的一种新的普适类。相变的分类是物理学的终极目标之一，而安德森相变无论是在理论上还是实验上都是最重要的相变之一尽管过去几十年来，在固态、原子、分子和光学系统中对无序拓扑系统中的输运现象进行了深入研究，但能带拓扑在安德森转变中的作用仍然不为人所知。尽管已经进行了深入而广泛的研究，但在相同的对称类和空间维度下，由拓扑引起的不同安德森相变的临界指数尚未被报道。在这篇论文中，肖振宇等人首次阐明了由拓扑引起的安德森转变的新普适类。

该论文以“手征对称类下的各向异性拓扑安德森相变”（Anisotropic topological Anderson transitions in chiral symmetry classes）为题，于2023年8月2日在线发表于《物理评论快报》（Physical Review

Letters）。进藤龙一是该论文的通讯作者，肖振宇为第一作者。这项工作的合作者还包括普林斯顿大学博士后川畑幸平（Kohei Kawabata）博士、量子材料科学中心毕业生骆训龙博士和上智大学教授大槻東巳（Tomi Ohtsuki）。上述研究工作得到了国家重点研发计划和国家自然科学基金委等支持。

论文链接：Zhenyu Xiao, Kohei Kawabata, Xunlong Luo, Tomi Ohtsuki, and Ryuichi Shindou, Anisotropic topological Anderson transition in chiral symmetry classes, Phys. Rev. Lett.131, 056301 (2023).https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.131.056301